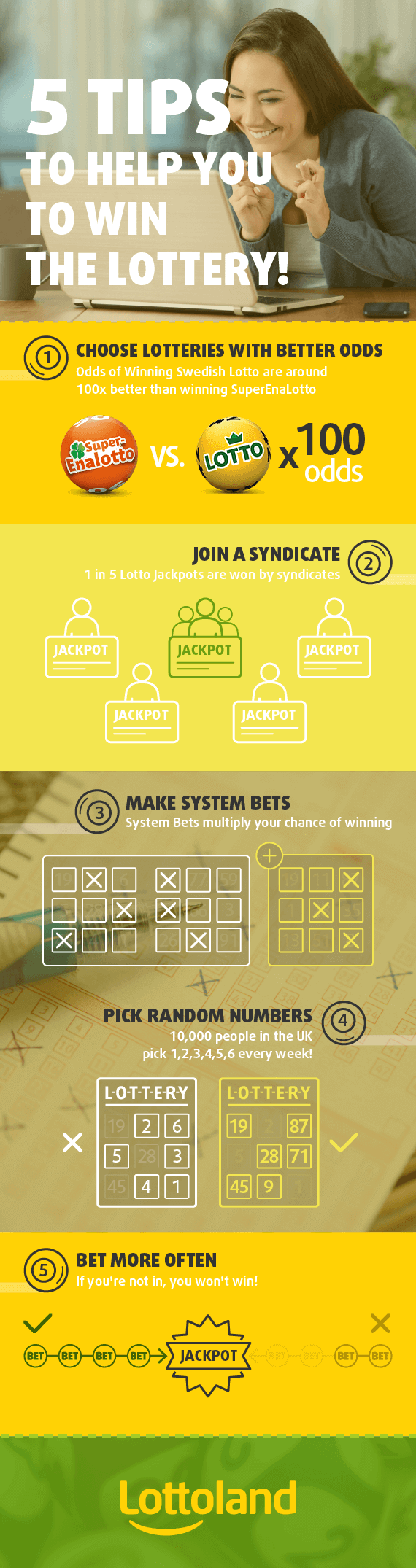
Which Lotto Game Has The Best Odds Of Winning
- Best Odds Lotto
- Which Lotto Game Has The Best Odds Of Winning
- Lottery Games With Best Odds
- What Lottery Game Has Best Odds Of Winning
- Lottery With The Best Odds Of Winning
Which Lottery Has the Best Jackpot Odds? The size of a lottery jackpot is what attracts most people to play the game. When the Powerball and Mega Millions lotteries offer billion-dollar jackpots, people everywhere will brave long lines to purchase tickets. When jackpots are that big, many who have never previously played the lottery. The absolute best any-prize odds of any of our lotteries is the French lotto, with any-prize odds of 6:1. In second place we have Austrian Lotto, another popular choice due to its low price, good any-prize and jackpot odds (the same as the Irish Lotto was before the 2015 changes), and added bonus game.
- Winning lottery ticket sold at Desert Hot Springs 7-Eleven store. A ticket with five numbers, but missing the Mega number, in Wednesday's SuperLotto Plus drawing was sold at a convenience store in Desert Hot Springs and is worth $18,452, the California Lottery.
- The absolute best any-prize odds of any of our lotteries is the French lotto, with any-prize odds of 6:1. In second place we have Austrian Lotto, another popular choice due to its low price, good any-prize.
When people ask “What are the Best Lottery Scratch off Odds?”, they usually are referring to the overall game odds. These are the printed odds on the back of instant scratch games. You might see something like “Overall Odds of Winning are 1 in 4.05”.
These are the the odds of winning any prize, including prizes that are equal to the price of the ticket.
One of our most popular scratcher strategies is our ranking of the best Overall Odds (available free to all our members) where players can instantly compare the overall odds for each game.
However, we are here to caution you that overall odds may not be the same as the best odds of winning. How so?
State lotteries can manipulate the overall odds to make them appear among the best when in reality, the individual prize odds might be among the worst.
Let’s dive in and see an example firsthand.
How is Overall Odds Calculated?
We need to take a step back and first see how does a state lottery calculate the overall odds of winning.
Best Odds Lotto
For every scratch game, the state lottery will determine the prize levels (e.g. $5, $10, $100, etc.) and the total number of prizes that will be made available. For our example, I’ve pulled an actual prize chart from a state lottery website.
As we can see, there are 12 different prize levels with a total of 2,395,512 prizes available. The lottery already tells us the overall odds of winning this game are 1 in 4.12, as show below.
The lottery calculated the “1 in 4.12” overall odds by dividing the total number of tickets printed by the total number of prizes available (2,395,512).
But we don’t know how many tickets were printed.
That’s right. The number of tickets printed isn’t disclosed, BUT we can figure it out by multiplying our total number of prizes (2,395,512) by the overall odds (4.12).
The result is approximately 9,900,000 tickets printed. Note we rounded the ticket count as it’s a rough estimate but close enough.
How about Prize Odds?
Now that we have the overall odds calculation out of the way, let’s dive a little deeper and see how the odds of each prize is calculated.
In our same game example, we see that the $500 prize will have 1,247 prizes available at the start of the game. Remember, the lottery has determined they are going to print 9,900,000 tickets so among all those tickets, there will 1,247 $500 winners.
To calculate the odds for our $500 prize, we simply divide the 9,900,000 printed tickets by the 1,247 prizes and learn the odds of winning the $500 prize are 1 in 7,915.
Pretty easy, right? Here’s what all the original prize odds look like.
Now that we know how the lottery calculates the odds, why shouldn’t we use the overall odds to figure out the best scratch off odds? Can’t we just see which game has the best overall odds and play that one?
Unfortunately not. Keep reading and let me show you a couple reasons why you shouldn’t rely only on the overall odds.
Is Winning Really Winning?
First, most players would agree that just getting their money back on a scratch ticket isn’t actually winning. “Winning” the price of the ticket back gives the illusion of winning and keep players coming back but it’s really just breaking even.
Let’s take a look at our same example from above and recalculate the odds of winning a prize more than the ticket price. You know, actually “winning”.
Which Lotto Game Has The Best Odds Of Winning
In this example, we want to know what are the real odds of winning any prize GREATER than $5, the price of our example ticket.
To do that, we’ll sum up the total number of prizes again but this time exclude all those breakeven $5 prizes.
With the $5 prizes removed, we now see there are really 1,407,930 actual winning prizes.
Using our math skills from above, we find that the actual winning odds, or as we call them Adjusted Odds, is really 1 in 7.01 tickets is a winner. That is 9,900,000 tickets divided by 1,407,930 total prizes.
The overall odds just change by OVER 70%!
Now some players may not care as getting their money back is winning in their mind. But let’s dive just a little deeper.
The Best Odds Illusion
I’ve just shown you that all those breakeven prizes aren’t really winning prizes but are there to make the overall odds seem better. Let’s go a step further and say a lottery wanted to really manipulate a scratch game to look better than it really is.
Lottery Games With Best Odds
Below is our original prize table from the example above, but I made 2 simple changes. I lowered the $250,000 top prize from 5 prizes down to just 1 and I lowered the second top prize, $10,000, from 24 prizes down to 2.
The change looks simple enough, the total prize count change is barely, if at all noticeable. The total number of prizes only went down by 26 prizes. However, let’s check out our prize odds.
We now see a HUGE change as the top prize odds went from 1 in 1,973,902 to now 1 in 9,869,509. A whopping 5x increase in odds!
The same thing for the $10,000 second place prize. We altered the count down to 2 prizes, which changed the odds from 1 in 411,230 to 1 in 4,934,755. This was a 12x increase in odds!
But here is the very sneaky part. Did you notice the overall odds?
The 1 in 4.12 overall odds never changed.
In both cases the lottery has two tickets with the same overall odds. If you had a choice though, which one would you choose?
For the curious, where did that extra prize money go? Remember, we took away 4 prizes of $250,000 and another 22 prizes of $10,000. You guessed it, pure lottery profit.
See, in our first example the total prize pool at the start of the game was $34,077,430, which represented an overall payout to players of 69.06%.
However, in our revised numbers, the prize pool dropped $1,230,000 to a total prize pool of $32,847,430, which is now only a payout of 66.58%.
The overall odds stayed the same but the lottery is keeping an extra $1,230,000 in profit instead of paying it to players.
Bringing it All Together
Let me show you one last example that brings both our points together. Let’s start with our original prize table again.
Now I’m going to reduce those top 2 prizes again like above BUT I’m also going to add some $5 prizes back. Let’s add 100,000 of the $5 prizes.
The lottery is still keeping a nice bonus profit by removing most of the top prizes but did shift a small piece of that money back to $5 prizes.
Here’s what our new prize table looks like
After taking out the top prizes and adding 100,000 small $5 prizes, we have a total prize count of 2,495,486. And now the magic.
Let’s divide the same ticket count by the new prize count. For those keeping track, that is 9,900,000 tickets divided by 2,495,486 total prizes. Our new overall odds of winning are 1 in 3.95!
Just like that I gave you a ticket with the best odds of winning, yet I took away most of the top prizes AND I’ve kept a bunch of extra ticket sales as pure profit!
Conclusion
Relying solely on the overall odds of scratchers as a way to determine the best odds of winning is a recipe for disaster.
The real “best odds of winning” will vary by the player and their own strategy.
Make sure to get a FREE account here at Lotto Edge. We offer lots of free tools to help you find the games with the best odds of winning for the strategies and prizes you want.
On This Page
Introduction
The California Lottery opened for business on October 3, 1985. Revenues from the lottery are directed towards education. The percentage directed towards prizes ranges from 48.5% to 79.7%, so you need to play the right game. Administrative expenses are supposed to be less than 13%. The time limit to cash a winning ticket is 180 days.
A unique feature of the California Lottery is that all games must be player against player and the state cannot have an interest in the outcome. For this reason, games based on random ball draws are all pari-mutual, which means the California Lottery takes a cut for schools and education and returns the rest to the winners. This is unlike other states that pay fixed prizes for some games.
The rest of this page contains my analysis of the several ways to play the California Lottery. However, for those who just want the executive summary, here is my advice:
- Don't play in the first place. Every state lottery offers terrible odds. With few exceptions, it is the worst bet you can make.
- If you must play, the best odds for bets under $5 is on the Hot Spot game, which claims to return 63.5% of money bet, which is better than the usual 50%.
- For bets of $5 or more, scratch cards offer the best value, with returns ranging from 67% to 80%, depending on the bet size.
- For games with the Second Chance option, don't forget to take it, which will give you about an additional 1.5% in return.
- For any game involving choosing numbers, I suggest the Quick Pick option. Players that pick their own numbers are at greater risk to get short changed on a jackpot by having to share it with many other players who picked the same numbers for the same reasons you did.
- If you play the Daily 3 or Daily 4, make Straight bets, as opposed to Box bets.
What follows is my analysis of each game.
Daily 3
The Daily 3 is a $1, twice daily game in which the player and lottery each pick three numbers from 0 to 9, with replacement.
Prizes are pari-mutual style, where the lottery takes a 50% cut (source: California Lottery Regulations, pages 21,22) of the total ticket sales and returns the rest to the winners.
The way each prize is determined is to take the dot product of the number of each type of win and the number of shares according to the table below. Then divide total prize money (48.5% of ticket sales) by the number of winning shares to determine the win per share. Prizes are rounded down to the nearest dollar with the breakage added to the Prize Reserve.
The following table shows the actual shares for each win as well as the mathematically fair number of shares, based on a box 1-2-3 ticket being 1 share. A 1-2-3 box ticket means one with three distinct numbers. A 1-1-2 box ticket means one with a pair of one digit, for example 8-5-8.
Daily 3 Shares
| Catch | Actual Shares | Fair Shares |
|---|---|---|
| Straight | 12.5 | 12 |
| Box (1-2-3) | 2 | 2 |
| Box (1-1-2) | 4 | 4 |
| Straight & box (1-2-3) win box only | 1 | 1 |
| Straight & box (1-1-2) win box only | 2 | 2 |
| Straight & box (1-2-3) win both | 7.25 | 7.25 |
| Straight & box (1-1-2) win both | 8.25 | 8.25 |
With both the Daily 3 and Daily 4, the shares given to straight bet players is disproportionately high. This means that box players are subsidizing straight players. Thus, my advice for Daily 3 players is to make straight bets only, if you must play.
The following table shows the probability of winning each prize, the average win, and return, based on an overall 50% return and assuming players bet equally between straight and box bets.
Daily 3 Return Table
| Bet | Probability | Average Win | Return |
|---|---|---|---|
| Straight | 0.001 | $510.20 | 51.02% |
| Box (1-1-2) | 0.003 | $163.27 | 48.98% |
| Box (1-2-3) | 0.006 | $81.63 | 48.98% |
Daily 4
The Daily 4 is a $1, daily game in which the player and lottery each pick four numbers from 0 to 9, with replacement. So, repeat numbers are possible.
Prizes are pari-mutual in nature, where the lottery returns approximately 48.5% of total money bet (source:California Lottery Regulations, page 17) of the total ticket sales. There is not a fixed pay table but how much you win will depend on how many other winners you will have to share with.
The way each prize is determined is to take the dot product of the number of each type of win and the number of shares according to the table below. Then divide total prize money (48.5% of ticket sales) by the number of winnings shares to determine the win per share. Prizes are rounded down to the nearest dollar with the breakage being added to the Prize Reserve.
The following table shows the actual shares for each win as well as the mathematically fair number of shares, based on a box 1-2-3-4 ticket being 0.5 shares. The numbers in parenthesis show an example of that type of box ticket. For example, 1-1-2-2 would have two each of two different digits, like 5-7-5-7.
Daily 4 Shares
| Catch | Actual Shares | Fair Shares |
|---|---|---|
| Straight | 12.5 | 12 |
| Box (1-2-3-4) | 0.5 | 0.5 |
| Box (1-1-2-3) | 1 | 1 |
| Box (1-1-2-2) | 2 | 2 |
| Box (1-1-1-2) | 3 | 3 |
| Straight & box (1-2-3-4) win box only | 0.25 | 0.25 |
| Straight & box (1-1-2-3) win box only | 0.5 | 0.5 |
| Straight & box (1-1-2-2) win box only | 1 | 1 |
| Straight & box (1-1-1-2) win box only | 1.5 | 1.5 |
| Straight & box (1-2-3-4) win both | 6.5 | 6.5 |
| Straight & box (1-1-2-3) win both | 6.75 | 6.75 |
| Straight & box (1-1-2-2) win both | 7.25 | 7.25 |
| Straight & box (1-1-1-2) win both | 7.75 | 7.75 |
The table above shows that a straight ticket pays 12.5 shares when a fair number of shares would be 12. This means that players betting box tickets are subsidizing straight ticket players. Thus, my advice for Daily 4 bettors is to make straight bets only.
The following table shows the probability of winning each prize, the average win, and return, based on an overall 50% return and assuming players bet equally between straight and box bets.
Daily 4 Return Table
| Bet | Probability | Average Win | Return |
|---|---|---|---|
| Straight | 0.0001 | $5,102.04 | 51.02% |
| Box (1-1-1-2) | 0.0004 | $1,224.49 | 48.98% |
| Box (1-1-2-2) | 0.0006 | $816.33 | 48.98% |
| Box (1-1-2-3) | 0.0012 | $408.16 | 48.98% |
| Box (1-2-3-4) | 0.0024 | $204.08 | 48.98% |
Fantasy 5
Fantasy 5 is a simple, $1 daily game where the player and lottery each pick 5 numbers from a range of 1 to 39. If the player matches at least three, then he wins instantly. Catching two wins a free game. If the player buys at least five tickets at once, then he will be entered into a 'second chance' game.
The percentage of ticket sales returned to winning players is 50% (source: California Lottery Regulations, page 25). That 50% is divided as follows:
- Match 5: 40%
- Match 4: 25%
- Match 3: 31%
- Match 2: Free play
- Reserve: 4%
This does not mean the odds are the same every game. Roughly 36% of the time nobody will match all five numbers, which will result in a larger prize pool in the following drawing. Naturally, large prize pools for matching all five numbers induces more competition from other players. Remember, much like poker and bingo, when it comes to the California Lottery, you're not playing against the lottery, but against the other players.
The following table shows the probability and contribution to the return for all possible outcomes, based on the 50% return percentage, the various prize shares, and the probability of each outcome. The wins shown are averages. I assume the 4% directed to the reserve goes to the other three cash prizes on a pro-rata basis. I also assume that if the player matches two numbers, for a free play, he will keep playing until he either wins something or loses. In other words, this table is on a 'bet resolved' basis.
Fantasy 5 Return Table
| Catch | Average Win | Combinations | Probability | Return |
|---|---|---|---|---|
| 5 | $107,482.71 | 1 | 0.000002 | 0.208333 |
| 4 | $395.16 | 170 | 0.000330 | 0.130208 |
| 3 | $14.85 | 5,610 | 0.010874 | 0.161458 |
| 0 to 1 | $0.00 | 510,136 | 0.988795 | 0.000000 |
| Total | 515,917 | 1.000000 | 0.500000 |
The probability of any win, assuming free plays are re-bet until resolved, is 1.12%.
SuperLotto Plus
This is a $1 game that generates the largest jackpots and is exclusive to California. It follows a format of choosing 5 'white' balls from 1 to 47 and one Mega Ball from 1 to 27. The jackpot is paid as a graduated annuity, meaning payments start out small and get larger, if the lump sum is not chosen.
The percentage of ticket sales returned to winning players is 50% (source: California Lottery Regulations, page 48). That 50% is divided as follows:
SuperLotto Plus — Prize Allocation

| Catch | Mega Ball | Probability |
|---|---|---|
| 5 | Yes | 60.50% |
| 5 | No | 3.00% |
| 4 | Yes | 1.50% |
| 4 | No | 2.50% |
| 3 | Yes | 2.25% |
| 3 | No | 11.00% |
| 2 | Yes | 6.00% |
| 1 | Yes | 5.75% |
| 0 | Yes | 4.50% |
| Reserve | 3.00% | |
| Total | 100.00% |
Based on a 50% return, the prize allocation above (assuming the reserve is spread on a pro-rata basis to the other prizes), and the probability of each prize, I show the following theoretical average wins for each prize.
SuperLotto Plus — Return Table
| Catch | Mega Ball | Average Win | Combinations | Probability | Return |
|---|---|---|---|---|---|
| 5 | Yes | $12,915,925 | 1 | 0.000000024 | 0.311856 |
| 5 | No | $24,633 | 26 | 0.000000628 | 0.015464 |
| 4 | Yes | $1,525 | 210 | 0.000005070 | 0.007732 |
| 4 | No | $97.75 | 5,460 | 0.000131832 | 0.012887 |
| 3 | Yes | $55.79 | 8,610 | 0.000207889 | 0.011598 |
| 3 | No | $10.49 | 223,860 | 0.005405111 | 0.056701 |
| 2 | Yes | $11.16 | 114,800 | 0.002771852 | 0.030928 |
| 1 | Yes | $2.19 | 559,650 | 0.013512778 | 0.029639 |
| 0 | Yes | $1.13 | 850,668 | 0.020539423 | 0.023196 |
| 0 to 2 | No | $0.00 | 39,653,068 | 0.957425392 | 0.000000 |
| Total | 41,416,353 | 1.000000000 | 0.500000 |
The probability of any win is 4.26%.
You can calculate the return for any given prizes with my SuperLotto Plus calculator.
Daily Derby
The Daily Derby is a $2, daily game in which the player chooses, in order, three numbers from 1 to 12, without replacement. In other words, the same way the player would bet a trifecta in a 12-horse race at the racetrack. In addition, the player must also pick three numbers from 0 to 9, with replacement, to represent the last three digits in the starting time of the race, which starts sometime between 1:40.00 and 1:49.00 PM. After betting closes, the Lottery will randomly choose the same things. If the player gets at least the winning horse or the race time, he will win something.
Before going further, let me review some horse racing terminology:
- Trifecta: Choosing the first three finishing horses, in order.
- Exacta: Choosing the first two finishing horses, in order.
- Win: Choosing the winning horse.

Prizes are pari-mutual style, where the lottery returns approximately 50% of total money bet (source: California Lottery Regulations, page 12) of the total ticket sales. Because it is pari-mutual, there is not a fixed pay table but how much you win will depend on how many other winners you will have to share with.
The following table shows how much of the prize pool is directed towards each type of win.
Daily Derby
| Win | Share of Prize Pool |
|---|---|
| Trifecta and time | 14% |
| Trifecta only | 36% |
| Exacta only | 16% |
| Win only | 25% |
| Time only | 5% |
| Reserve | 4% |
If the player wins for both the win or exacta and the time, then he shall be paid for both. For example, on the April 5, 2016 drawing a win for the winning horse only paid $3 and the race time only paid $56. So, a win for both paid $59.
The next table shows the probability, average win, and contribution to the return for each type of win. I assume the 4% directed towards the reserve is distributed on a pro-rata basis to the other wins, according to win share. The return column is the product of the average win, probability, and 0.5. The reason for dividing by 2 is the ticket cost is $2, and I'm trying to show the return per dollar bet.
Daily Derby Return Table
| Event | Average Win | Combinations | Probability | Return |
|---|---|---|---|---|
| Trifecta & time | $192,500.00 | 1 | 0.00000076 | 0.072917 |
| Exacta & time | $80.80 | 9 | 0.00000682 | 0.000275 |
| Win & time | $59.90 | 100 | 0.00007576 | 0.002269 |
| Time only | $56.48 | 1,210 | 0.00091667 | 0.025887 |
| Trifecta | $492.54 | 999 | 0.00075682 | 0.186383 |
| Exacta | $24.32 | 8,991 | 0.00681136 | 0.082837 |
| Win only | $3.42 | 99,900 | 0.07568182 | 0.129433 |
| Loser | $0.00 | 1,208,790 | 0.91575000 | 0.000000 |
| Total | 1,320,000 | 1.00000000 | 0.500000 |
Hot Spot
This is a keno game played every four minutes from 6 AM to 2 AM every day. The player may bet $1 to $20 per game. As in conventional keno, the player picks 1 to 10 numbers from a range of 1 to 80. The Lottery selects 20 numbers from the same range. The more numbers the player picked that match the Lottery draw, the more he will win.
Prizes are pari-mutual style, where the lottery returns 63% of total money bet to winners (source: California Lottery Regulations, page 28) of the total ticket sales. In other words, there is not a fixed pay table but how much you win will depend on how many other winners you will have to share with. Often, there are no winners for long-shot wins. The rules are rather complicated, but basically prize pools carry over to the next game for any given type of win if there were no winners.
The following table shows the probability of any given win according to the number of picks and the number that match the Lottery draw.
Hot Spot ProbabilitiesExpand
| Catch | Pick 1 | Pick 2 | Pick 3 | Pick 4 | Pick 5 | Pick 6 | Pick 7 | Pick 8 | Pick 9 | Pick 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 in 11.3 | 1 in 15.7 | 1 in 21.8 | |||||||
| 1 | 1 in 4 | |||||||||
| 2 | 1 in 16.6 | 1 in 7.2 | 1 in 4.7 | |||||||
| 3 | 1 in 72.1 | 1 in 23.1 | 1 in 11.9 | 1 in 7.7 | 1 in 5.7 | |||||
| 4 | 1 in 326 | 1 in 82.7 | 1 in 35 | 1 in 19.2 | ||||||
| 5 | 1 in 1551 | 1 in 323 | 1 in 116 | 1 in 54.6 | 1 in 30.7 | 1 in 19.4 | ||||
| 6 | 1 in 7753 | 1 in 1366 | 1 in 423 | 1 in 175 | 1 in 87.1 | |||||
| 7 | 1 in 40979 | 1 in 6232 | 1 in 1690 | 1 in 621 | ||||||
| 8 | 1 in 230115 | 1 in 30682 | 1 in 7384 | |||||||
| 9 | 1 in 1380688 | 1 in 163381 | ||||||||
| 10 | 1 in 8911711 |
There is another keno-based game called the Bulls Eye. In this game, the first number drawn by the Lottery must match one of the player's picks. If it does, the player will automatically win something, depending on the number of other balls in the draw that match his other picks. If not, he is an automatic loser.
The player may not play the Bulls Eye alone but may play it on a 50/50 basis with the Hot Spot game, if he wishes. The California Lottery web site does not indicate the return percentage of the Bulls Eye game, so you're on your own with that one.
The following table shows the probability of each possible win in the Bulls Eye game. The 'Catch' column refers to the number of picks the player matches to the Lottery draw, not including the first ball.
Bulls Eye ProbabilitiesExpand
| Catch | Pick 1 | Pick 2 | Pick 3 | Pick 4 | Pick 5 | Pick 6 | Pick 7 | Pick 8 | Pick 9 | Pick 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 in 80 | 1 in 52.7 | 1 in 46.4 | 1 in 46.2 | 1 in 49.3 | 1 in 55 | 1 in 63.5 | 1 in 75.1 | 1 in 90.6 | 1 in 111 |
| 1 | 1 in 166 | 1 in 72.1 | 1 in 47 | 1 in 37 | 1 in 32.4 | 1 in 30.6 | 1 in 30.5 | 1 in 31.6 | 1 in 33.9 | |
| 2 | 1 in 480 | 1 in 154 | 1 in 79.4 | 1 in 51.4 | 1 in 38.1 | 1 in 31 | 1 in 27.1 | 1 in 24.9 | ||
| 3 | 1 in 1632 | 1 in 413 | 1 in 175 | 1 in 95.8 | 1 in 61.3 | 1 in 43.8 | 1 in 33.9 | |||
| 4 | 1 in 6202 | 1 in 1292 | 1 in 463 | 1 in 219 | 1 in 123 | 1 in 77.8 | ||||
| 5 | 1 in 25843 | 1 in 4553 | 1 in 1408 | 1 in 583 | 1 in 290 | |||||
| 6 | 1 in 117084 | 1 in 17806 | 1 in 4829 | 1 in 1773 | ||||||
| 7 | 1 in 575287 | 1 in 76705 | 1 in 18461 | |||||||
| 8 | 1 in 3068195 | 1 in 363070 | ||||||||
| 9 | 1 in 17823422 |
The regulations for Hot Spot are confusing when it comes to how the prizes are determined. However, they do kindly indicate 'Typical Prize Amounts' for the Hot Spot game on page 29 of the Regulations, as follows:
Hot Spot Typical Prize AmountsExpand
| Catch | Pick 1 | Pick 2 | Pick 3 | Pick 4 | Pick 5 | Pick 6 | Pick 7 | Pick 8 | Pick 9 | Pick 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | $0 | $0 | $0 | $0 | $0 | $0 | $0 | $1 | $1 | $3 |
| 1 | $2 | $0 | $0 | $0 | $0 | $0 | $0 | $0 | $0 | $0 |
| 2 | $9 | $2 | $1 | $0 | $0 | $0 | $0 | $0 | $0 | |
| 3 | $26 | $5 | $2 | $1 | $1 | $0 | $0 | $0 | ||
| 4 | $75 | $16 | $5 | $3 | $0 | $0 | $0 | |||
| 5 | $450 | $60 | $10 | $10 | $5 | $2 | ||||
| 6 | $900 | $150 | $75 | $25 | $15 | |||||
| 7 | $2000 | $575 | $125 | $40 | ||||||
| 8 | $10000 | $2750 | $575 | |||||||
| 9 | $30000 | $5000 | ||||||||
| 10 | $100000 |
When these typical prize amounts are applied to the probability of winning, it results in returns of less than the 63% claimed in the Regulations. What does the Lottery do with the extra money? The Regulations say, 'The Director will prevent the Wagered Prize Fund from exceeding $2.9 million through augmentation of Prizes and implementation of Promotions, including the issuance of free Hot Spot tickets, from time to time.' -- Section 3.5.4.B(2), page 29.
The Regulations also state 'Typical Prize Amounts' for the Bulls Eye game (section 3.5.6.C(1)), as follows:
Bulls Eye Typical Prize AmountsExpand
| Catch* | Pick 1 | Pick 2 | Pick 3 | Pick 4 | Pick 5 | Pick 6 | Pick 7 | Pick 8 | Pick 9 | Pick 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | $44 | $12 | $6 | $4 | $3 | $4 | $4 | $4 | $4 | $4 |
| 1 | $55 | $15 | $10 | $6 | $2 | $2 | $2 | $2 | $2 | |
| 2 | $125 | $30 | $12 | $5 | $2 | $2 | $2 | $2 | ||
| 3 | $200 | $60 | $30 | $15 | $5 | $5 | $2 | |||
| 4 | $500 | $150 | $50 | $35 | $10 | $5 | ||||
| 5 | $1000 | $350 | $100 | $50 | $35 | |||||
| 6 | $6000 | $675 | $275 | $100 | ||||||
| 7 | $18500 | $3000 | $750 | |||||||
| 8 | $35000 | $10000 | ||||||||
| 9 | $200000 |
*: The Catch column does not include the Bulls Eye ball.
The final table on this game shows the return of both the Hot Spot and Bulls Eye bets according to the number of picks, based on the Typical Prize Amounts in the Regulations and the probability of winning. I know these fall short of the 63.5% return claimed, but the Regulations don't give me enough information to analyze this one properly.
Hot Spot and Bulls Eye Returns
| Pick | Hot Spot | Bulls Eye |
|---|---|---|
| 1 | 50.00% | 55.00% |
| 2 | 54.11% | 55.85% |
| 3 | 63.83% | 59.76% |
| 4 | 65.86% | 61.63% |
| 5 | 65.16% | 59.99% |
| 6 | 57.43% | 55.77% |
| 7 | 57.66% | 57.35% |
| 8 | 58.45% | 56.61% |
| 9 | 55.51% | 57.01% |
| 10 | 59.66% | 55.47% |
Scratchers
Scratch card games are simple games on a card. The player scratches to reveal his prize. At the time of this writing, scratch cards were available at costs of $1, $2, $5, $10, $20, and $30.
The Lottery doesn't implicitly state the percentage of money returned to the player. However, they kindly indicate the number of tickets printed and the odds of winning, which is enough to calculate the return percentage. Let's look at the Year of the Monkey $1 game, as an example. They tell us everything we need to know, except the numbers of losing tickets. We can get at the total number of all tickets printed by multiplying the number printed for any given win by the inverse of the probability of winning. For example, there were 38 $800 tickets printed. The probability of winning is 1/487263. So, the total tickets printed is 38*487,263 = 18,515,994.
Next, let's subtract out the 'ticket' winners, under the assumption the player will keep playing until he either wins some money or loses. They tell us the number of ticket wins is 1,555,344. So, the sum of monetary wins and losses is 18,515,994 - 1,555,344 = 16,960,650. The total monetary wins is 2,319,026. That leaves 16,960,650 - 2,319,026 = 14,641,624 losers.
We can now set up a return table for the game, as follows:
Year of the Monkey
| Win | Tickets | Probability | Return |
|---|---|---|---|
| 800 | 38 | 0.000002 | 0.001792 |
| 100 | 495 | 0.000029 | 0.002919 |
| 40 | 7,684 | 0.000453 | 0.018122 |
| 20 | 44,439 | 0.002620 | 0.052402 |
| 10 | 162,950 | 0.009608 | 0.096075 |
| 5 | 399,916 | 0.023579 | 0.117895 |
| 4 | 592,502 | 0.034934 | 0.139736 |
| 2 | 1,111,002 | 0.065505 | 0.131009 |
| Loser | 14,641,624 | 0.863270 | 0.000000 |
| Total | 18,515,994 | 1.000000 | 0.559951 |
The lower right cell shows the Year of the Monkey game has a return of 56.00%. The probability of any win is 100% - 86.33% = 13.67%.
However, not all games have the same return. As a rule of thumb, for any given denomination, returns are in a tight range. As you pay for more a ticket, the return percentage goes up. Here is the average return of some games I sampled, by denomination:
Scratch Card Average Returns
| Bet | Average Return |
|---|---|
| $1 | 56.75% |
| $2 | 61.95% |
| $5 | 66.97% |
| $10 | 72.95% |
| $20 | 76.22% |
| $30 | 79.72% |
I'm sure some people will not appreciate my mentioning this, but there is a potential advantage play in scratch card games. The California Lottery is nice enough to indicate how many tickets for each win have already been cashed. If there is a game that is almost sold out, as evidenced by the small wins, with a high ratio of large wins still unclaimed, then it may mean the remaining unsold tickets are rich in big winners. The same principle as card counting in blackjack. I'll leave the details to the reader (don't you hate it when I say that?).
Multi-State Games
California participates in part of both multi-state lotteries, the Powerball and Mega Millions.
According to Lottery regulations, approximately 50% of money bet is returned to winning players source: California Lottery Regulations, page 36, 42). Unlike other states that participate in these games, all prizes in California are on a pari-mutual basis. However, the big jackpot will be the same as it is in the other states, at any given time.
Please see my Powerball page for more information on that game. A Mega Millions page is coming soon.
Second Chance
What Lottery Game Has Best Odds Of Winning
Losing Scratchers, Fantasy 5, and SuperLotto Plus tickets are eligible to enter a weekly second chance drawing. To enter the drawing, the bettor must open an account through the California Lottery web site and submit the losing ticket numbers. In the unlikely chance the player wins anything in the weekly drawing, he will be alerted by Email.
Based on a randomly-chosen week, I estimate players bet $2,561,530 on Fantasy 5 tickets. The second chance drawing for that game pays out $42,000, for an additional return to the player of 1.64%.
By similar math, for the SuperLotto Plus, I show $5,044,584 in ticket sales and $75,000 in prizes for an additional 1.49% of money bet returned to the player.
I do not know the return paid to Scratchers players, but assume it to be about the same.
Of course, to have a chance at a Second Chance, you have to enter. The expected return will be greater than the figures above according to how many other losers don't bother to enter the Second Chance drawing, as you are competing against only players that enter.
Internal Links
External Links
- California Lottery — Official web site.
- California Lottery Regulations — The fine print of the game rules.
- Wikipedia — Page on the California Lottery